RSA加密学习
简介:
RSA公开密钥密码体制是一种使用不同的加密密钥与解密密钥
“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制
算法原理:
根据数论,寻求两个大素数比较简单,而将他们的乘积进行因式分解却极其困难,因此可以将成绩公开作为解密密钥。
算法描述:
(1)任意选取两个不同的大素数p和q计算乘积n = pq。
(2)根据欧拉函数,求得**r=φ(N)=φ(p)φ(q)=(p-1)(q-1)**。
(3)任意选取一个大整数e,满足gcd(e,φ(N))=1,整数e用做加密钥(注意:e的选取是很容易的,例如,所有大于p和q的素数都可用)
(4)确定的解密钥d,满足 (de)modφ(N) = 1 ,即de = kφ(N) + 1,k>=1是一个任意的整数;所以,若知道e和φ(N),则很容易计算出d
(5)将明文m加密成密文c,加密算法为:
c = E(m) = m^e mod n
(6)将密文c解密为明文m,解密算法为:
m = D(c) = c^d mod n
各类RSA题型及解密脚本
Python 脚本前置环境
gmpy库安装
1.Python3 安装:Python官网
2.cmd中输入wheel检查python是否安装了wheel文件包,wheel安装指令:pip install wheel
3.安装与python版本一致的gmpy2的whl文件whl文件下载
4.cmd中输入pip install 'whl文件的绝对路径'安装whl文件包
5.输入pip install gmpy2安装gmpy2,可以在python交互环境下输入import gmpy2检查

crypto库安装
1.cmd中输入pip install pycryptodome -i https://pypi.tuna.tsinghua.edu.cn/simple
2.在本地Python/lib/site-packages中将crypto文件夹的c改成C:

同样可以在python的交互界面输入import Crypto进行检查:
已知p,q,e(e,n,c)求m
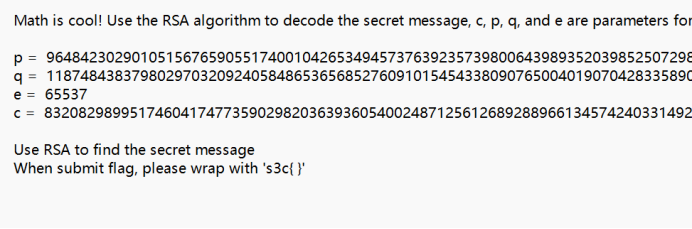
例题来源:S3C 2022三月队内赛
题目如下:
解密脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
| import libnum
from Crypto.Util.number import long_to_bytes
c =
n =
e =
q =
p =
d = libnum.invmod(e,(p-1)*(q-1))
m = pow(c,d,n)
string = long_to_bytes(m)
print(string)
|
已知c,d,n求m
解密脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| import gmpy2
def Decrypt(c,e,p,q):
L=(p-1)*(q-1)
d=gmpy2.invert(e,L)
n=p*q
m=gmpy2.powmod(c,d,n)
flag=str(m)
print("flag{"+flag+"}")
if __name__ == '__main__':
p =
q =
e =
c =
Decrypt(c,e,p,q)
|
已知 n,e,c,dp求m
解密脚本如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| import gmpy2
import rsa
import binascii
p=0
e=65537
n = 85413323752199019806030766630760449394238054889872415531186815348349883843039718091361611175963675771467536496812507338620957273406076058263122453235926619595761737396698699834116678598534261542535530241537247151318756003375573850725841254167462648747492270335084402716816450008370008491069875351593380154253
dp = 1576424214336939000475035870826282526256046059505538052583882122452307602095912733650442447289122473348318614749578285418144935611098423641334952097553125
c = 53653254613997095145108444611576166902006080900281661447007750088487109015427510365774527924664116641019490904245926171500894236952984157500461367769566121581870986304353174732328118576440353500038670030097108081972287049673200783198844842527470746431369314585103203118824985764754487936404004696485346196488
temp=dp*e
for i in range(1,e) :
if (temp-1)%i==0:
x=(temp-1)//i+1
y=n%x
if y==0:
p=x
break
q=n//p
d=gmpy2.invert(e,(p-1)*(q-1))
key=rsa.PrivateKey(n,e,d,p,q)
m=pow(c,d,n)
print(binascii.unhexlify(hex(m)[2:]))
|






